| Username |
Post |
| Gokul |
Posted
on 10-Feb-04 06:53 AM
For fun,

|
| arnico |
Posted
on 10-Feb-04 07:14 AM
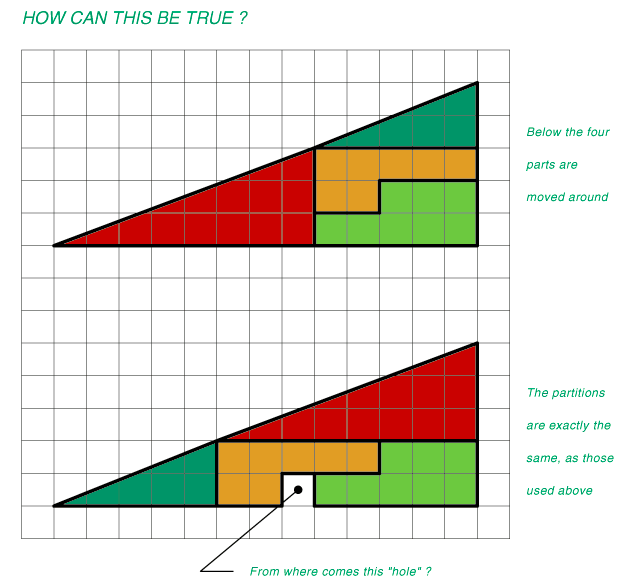
The short answer is that the overall shape is NOT a triangle.
|
| arnico |
Posted
on 10-Feb-04 07:17 AM
The short answer is that the overall shape is not a triangle, and even if the missing gap were filled in, the two figures have different shapes.
To see why, study the two smaller triangles.
Notice that the green one has a tangent of 2/5 = 0.4
The red triangle has a tangent of 3/8 = 0.375.
Take the arctan of each and you see that the only angle that is the same in the two triangles is the right angle.
|
| DWI |
Posted
on 10-Feb-04 07:29 AM
Absolutely right Arnico.
There is a slight difference in the angles.
If you don't wanna measure the angles, you can just observe one of the key blocks.
Starting from left, observe the 5th green block. Right above this block is another partially colored green block. Notice how the green color completely touches all three corner of the rectangle (the block itself). However, compare this block to the respective block in the figure above (same position) and notice the red block only covers lower two corner of the block, the upper two corner are untouched.
The angle is slightly different.
|
| thaag |
Posted
on 10-Feb-04 07:41 AM
You can see visible difference at points A B C
Tan a=p/b
a=inv(tan p/b)
a=inv(tan 3/8)
a=20.556 degrees
tan b=p/b
b=inv(tan p/b)
b=inv(tan 2/5)
b=21.801 degrees
Not the same

|
| thaag |
Posted
on 10-Feb-04 07:47 AM
missed lines sorry!

|
| Biswo |
Posted
on 10-Feb-04 02:26 PM
I had a quick peek at Gokul's original graph. I was wondering how the two 'mega' triangles have same perpendicular, same base, but different hypotenuse?
--
In a related note, the evolution of math has an interesting aspect: pythagorus theorem was discovered, presumably, before the discovery of algebraic number. So, those who went on to measure the hypotenuse of a triange with base 1, perpendicular 1 had this big time trouble:they couldn't accurately measure its hypotenuse (sth about 1.4).
Later, some of the mathematicians theorized that you can't exactly draw a triangle of base 1 and perpendicular 1 and that has right angle between them. After all, you can't measure it, you can't draw it.It made perfect sense to them.Hmm.
Hence the discovery of algebraic number, aka numbers like pi, square root two, made the life a lot easier. It was the story I was told by my math teacher long ago in China and the credit goes to him:-)
In the current age, if we have been able to see further, it is by standing on the shoulders of the giants. Like Pythogorus, and the fella who discovered algebraic numbers, but didn't have his name on it.Science may or may not have opened the door of infinite wisdom, it surely has stopped us from making infinite errors.
|
| DWI |
Posted
on 10-Feb-04 05:23 PM
Soon as I posted my explanation, I had the same question Biswo had.
How can two triangles have same base, same height and different hypotenuse. In essence, we have two different area for two triangles that have same base and same height. We all know
Area of a triangle= 1/2 (Base * Height)
Now, how could these two triangles have different area, when their bases and heights are equal?
I am still thinking, I am definately missing a big picture. Rescue me out, before I do it myself.
|
| thaag |
Posted
on 10-Feb-04 06:16 PM
DWI,
This is just an optical illusion. All it has to do with the point where red triangle ends and green triangle begins. which can not be at same point.
|
| acharya |
Posted
on 10-Feb-04 06:22 PM
I second thaag.
|
| DWI |
Posted
on 10-Feb-04 08:27 PM
Thaag,
Thanks. But that was my explanation initially too.
Agreed the colored squares are optical illusions, but for a second forget the main question of this thread.
How can we have same base, same heights but different angle in two triangles.
It could be because the sides of the triangle are drawn with thick line which can easily accomodate the angular difference.
Agree?
|
| arnico |
Posted
on 10-Feb-04 08:32 PM
The point is that the big shapes in the two pictures are NOT triangles.
There is a "kink" where the red triangle starts and the green one ends... the "hypotenuse" of the large "triangles" is not a straight line.
|
| Biswo |
Posted
on 10-Feb-04 09:47 PM
Yes, the kinks are not so visible. They look like straight lines.
|
| Rusty |
Posted
on 11-Feb-04 06:00 AM
I think Arnico answers the question. Both triangles(big shapes) are not triangles because if you observe them closly, their hypotenuses are not stright line. I think the following link answers this question...
http://www.grand-illusions.com/triangle1.htm
Sorry for providing the answer for this illusion. Fun is gone now:)
|

